

Conversely, if the base angles of a triangle are equal, then the triangle is isosceles.” Isosceles triangle theorem states that “In an isosceles triangle, the angles opposite to the equal sides are equal.Therefore ∆ABC is an Isosceles triangle.Īpplying Pythagoras theorem in ∆ABD, we have If two sides are equal, then the angles opposite to these sides are also equal.įor example, in the following triangle, AB = AC. Now, let us understand the definition of an isosceles triangle.Ī triangle is said to be an Isosceles triangle if its two sides are equal. Also, ancient Babylonian and Egyptian mathematicians were of the know-how on the calculations required to find the ‘area’ much before the ancient Greek mathematicians started studying the isosceles triangle. The term isosceles triangle is derived from the Latin word ‘īsoscelēs’, and the ancient Greek word ‘ἰσοσκελής (isoskelḗs)’ which means “equal-legged”. The three sides of the triangle above are AB, BC and AC. An exterior angle of a triangle is formed by any side of a triangle and the extension of its adjacent side. These angles are also called the interior angles of a triangle. The angle formed at A can also be written as ∠BAC. The three angles are the angles made at these vertices, i.e. And we use that information and the Pythagorean Theorem to solve for x.In the above triangles, the three vertices are A, B and C. So this is x over two and this is x over two. Two congruent right triangles and so it also splits this base into two. So the key of realization here is isosceles triangle, the altitudes splits it into
#AREA OF ISOSCELES TRIANGLE PLUS#
So this length right over here, that's going to be five and indeed, five squared plus 12 squared, that's 25 plus 144 is 169, 13 squared. This distance right here, the whole thing, the whole thing is So x is equal to the principle root of 100 which is equal to positive 10. But since we're dealing with distances, we know that we want the This purely mathematically and say, x could be Is equal to 25 times four is equal to 100. Make sure the arc passes at least halfway across the base. Sweep the compass in the space above the base, drawing an arc.
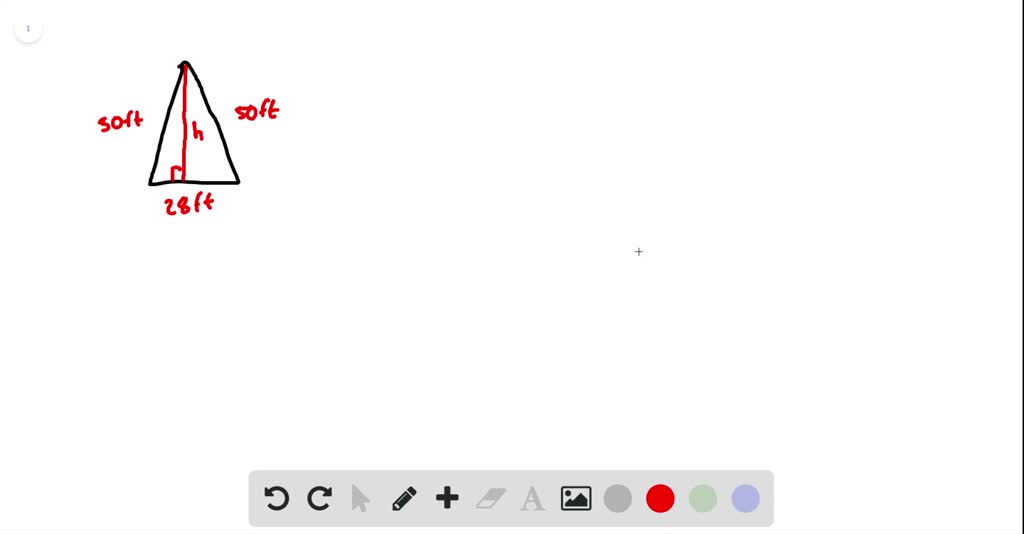
The angle opposite the base is called the vertex angle, and the angles opposite the legs are called base angles. To do this, place the tip of the compass on one of the base’s endpoints. Parts of an isosceles triangle For an isosceles triangle with only two congruent sides, the congruent sides are called legs. We can multiply both sides by four to isolate the x squared. Or, if provided a line segment, set the compass to the segments length. So subtracting 144 from both sides and what do we get? On the left hand side, we have x squared over four is equal to 169 minus 144. The area of an isosceles triangle is the amount of surface or space enclosed between the sides of the isosceles triangle. That's just x squared over two squared plus 144 144 is equal to 13 squared is 169. Definition of Area of Isosceles Triangle A triangle in which two sides (legs) are equal and the base angles are equal is known as an isosceles triangle. This is just the Pythagorean Theorem now. We can write that x over two squared plus the other side plus 12 squared is going to be equal to We can say that x over two squared that's the base right over here this side right over here. If you know one leg a and the hypotenuse c, use the formula: area a × (c² - a²) / 2. Find the length of the other two sides and the area of the triangle. If you know the two legs, then use the formula area a × b / 2, where a, and b are the legs. Let's use the Pythagorean Theorem on this right triangle on the right hand side. The semi-perimeter of an isosceles triangle is 15 cm, and the length of the unequal side is 12 cm. And so now we can use that information and the fact and the Pythagorean Theorem to solve for x. So this is going to be x over two and this is going to be x over two. So they're both going to have 13 they're going to have one side that's 13, one side that is 12 and so this and this side are going to be the same. And since you have twoĪngles that are the same and you have a side between them that is the same this altitude of 12 is on both triangles, we know that both of these So that is going to be the same as that right over there. Because it's an isosceles triangle, this 90 degrees is the The formula for finding the area of an obtuse triangle is expressed as 1/2 bh. Is an isosceles triangle, we're going to have twoĪngles that are the same. The height of an obtuse isosceles triangle may be found in the same way. Well the key realization to solve this is to realize that thisĪltitude that they dropped, this is going to form a right angle here and a right angle here and notice, both of these triangles, because this whole thing To find the value of x in the isosceles triangle shown below.


 0 kommentar(er)
0 kommentar(er)
